Tilt correction¶
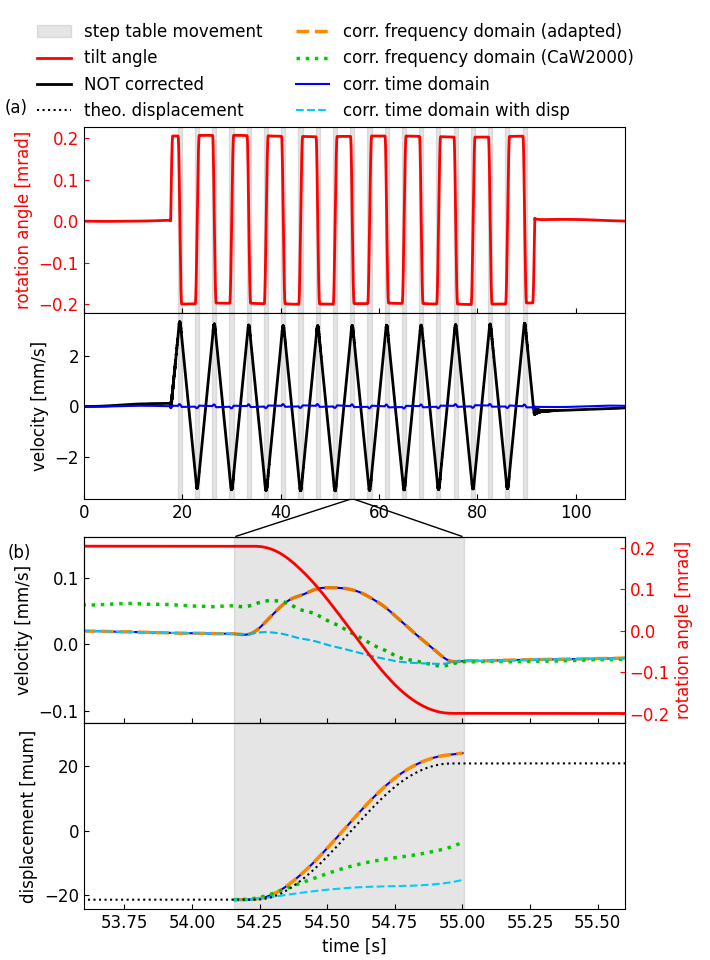
This script implements a simple example for dynamic tilt correction. It reproduces the tilt table experiment from [BernauerEtAl2020] based on the method by [CrawfordAndWebb2000].
The example demonstrates the different correction variants provided by
owlpy.tilt.correction.remove_tilt().
The example data required by this script is included in the OwlPy example data
collection. It can be downloaded with the script get_example_data.sh.
#!/usr/bin/env python
import os
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import rc
from obspy import Stream, Trace
# from matplotlib.pylab import *
from owlpy.tilt.util import (
get_data, trigger, calc_residual_disp, get_angle,
theo_resid_disp, calc_height_of_mass)
from owlpy.tilt.correction import remove_tilt
from matplotlib.transforms import (
Bbox, TransformedBbox, blended_transform_factory)
from mpl_toolkits.axes_grid1.inset_locator import (
BboxPatch, BboxConnector, BboxConnectorPatch)
# this script implements a simple example for dynamic tilt correction. It
# reproduces the # tilt table experiment from Bernauer et al. 2020 (SRL).
data_dir = 'data/tilt_correction_step_table'
# this method is needed for the matplotlib zoom effect
def connect_bbox(
bbox1, bbox2, loc1a, loc2a, loc1b, loc2b, prop_lines,
prop_patches=None):
if prop_patches is None:
prop_patches = {
**prop_lines,
"alpha": prop_lines.get("alpha", 1) * 0.0,
}
c1 = BboxConnector(bbox1, bbox2, loc1=loc1a, loc2=loc2a, **prop_lines)
c1.set_clip_on(False)
c2 = BboxConnector(bbox1, bbox2, loc1=loc1b, loc2=loc2b, **prop_lines)
c2.set_clip_on(False)
bbox_patch1 = BboxPatch(bbox1, **prop_patches)
bbox_patch2 = BboxPatch(bbox2, **prop_patches)
p = BboxConnectorPatch(bbox1, bbox2,
loc1a=loc1a, loc2a=loc2a, loc1b=loc1b, loc2b=loc2b,
**prop_patches)
p.set_clip_on(False)
return c1, c2, bbox_patch1, bbox_patch2, p
# this method is needed for the matplotlib zoom effect
def zoom_effect01(ax1, ax2, xmin, xmax, **kwargs):
"""
Connect *ax1* and *ax2*. The *xmin*-to-*xmax* range in both axes will
be marked.
Parameters
----------
ax1
The main axes.
ax2
The zoomed axes.
xmin, xmax
The limits of the colored area in both plot axes.
**kwargs
Arguments passed to the patch constructor.
"""
trans1 = blended_transform_factory(ax1.transData, ax1.transAxes)
trans2 = blended_transform_factory(ax2.transData, ax2.transAxes)
bbox = Bbox.from_extents(xmin, 0, xmax, 1)
mybbox1 = TransformedBbox(bbox, trans1)
mybbox2 = TransformedBbox(bbox, trans2)
prop_patches = {**kwargs, "ec": "none", "alpha": 0.0}
c1, c2, bbox_patch1, bbox_patch2, p = connect_bbox(
mybbox1, mybbox2,
loc1a=3, loc2a=2, loc1b=4, loc2b=1,
prop_lines=kwargs, prop_patches=prop_patches)
ax1.add_patch(bbox_patch1)
ax2.add_patch(bbox_patch2)
ax2.add_patch(c1)
ax2.add_patch(c2)
ax2.add_patch(p)
return c1, c2, bbox_patch1, bbox_patch2, p
# this method is needed for the matplotlib zoom effect
def zoom_effect02(ax1, ax2, **kwargs):
"""
ax1 : the main axes
ax1 : the zoomed axes
Similar to zoom_effect01. The xmin & xmax will be taken from the
ax1.viewLim.
"""
tt = ax1.transScale + (ax1.transLimits + ax2.transAxes)
trans = blended_transform_factory(ax2.transData, tt)
mybbox1 = ax1.bbox
mybbox2 = TransformedBbox(ax1.viewLim, trans)
prop_patches = {**kwargs, "ec": "none", "alpha": 0.2}
c1, c2, bbox_patch1, bbox_patch2, p = connect_bbox(
mybbox1, mybbox2,
loc1a=2, loc2a=3, loc1b=1, loc2b=4,
prop_lines=kwargs, prop_patches=prop_patches)
ax1.add_patch(bbox_patch1)
ax2.add_patch(bbox_patch2)
ax2.add_patch(c1)
ax2.add_patch(c2)
ax2.add_patch(p)
return c1, c2, bbox_patch1, bbox_patch2, p
##################################
# TEST - tilt table - #
# - high gain, 1/6 - #
# - 166.7mum - #
# - 21 steps - #
##################################
# get raw data from
stream1 = os.path.join(data_dir, 'XX.TC120..HH*.D.2018.343')
stream2 = os.path.join(data_dir, 'XX.BS1..HJ*.D.2018.343')
# at the time
utctime = '2018-12-09T19:48:48.6'
# how many seconds of data do you want to read in?
duration = 120
# define the seismometer and rotational sensor stream identifiers
correct_channel = 'HH*'
input_channel = 'HJ*'
# set some trigger parameters
# start to search for steps from second
S = 18.0
# no steps after second
E = 91.0
# correct the trigger onset by a constant offset, which was determined visually
c_on = -0.075
c_off = 0.49
# define the zoom windows for the plots
zoom00 = 0.0
zoom01 = 110.0
zoom0 = 53.6
zoom1 = 55.6
# geometrical parameters of the experiment
# horizontal distance of center of seismometer to axis of rotation in m
l = 0.32 # noqa
# vertical distance of bottom of seismometer to axis of rotation in m
dh = 0.047
# define the source stream (ss) and the receiver stream (sr) channels
ch_sr = 'HHN'
ch_ss = 'HJE'
# get the data
vel_orig, rr_orig = get_data(
stream1, stream2, utctime, duration, correct_channel, input_channel,
os.path.join(data_dir, 'station.xml'), ch_sr, ch_ss)
# make four independent streams containing tilt contaminated acceleration
# recordings:
# (1) the original tilt contaminated stream for later comparisons
# (2) the stream that will be treated with the frequency domain (CaW)
# correction
# (3) the stream that will be treated with the frequency domain (coh)
# correction
# (4) the stream that will be treated with the time domain correction
sr = vel_orig.copy()
sr.filter('bandpass', freqmin=0.03, freqmax=10, corners=8, zerophase=True)
acc_orig = sr.copy()
acc_orig.differentiate() # original acc recording (reciever)
rf1 = sr.copy()
rf2 = sr.copy()
rt = sr.copy()
rf1.differentiate() # reciever for freq-domain (coh) analysis (acc recording)
rf2.differentiate() # reciever for freq-domain (plain) analysis (acc recording) # noqa
rt.differentiate() # reciever for time-domain analysis (acc recording)
# make two independent streams containing the tilt angle recording
# (1) original tilt angle recording for later comparisons
# (2) tilt angle recording as the source for the corrections
ss = rr_orig.copy()
ss.filter('bandpass', freqmin=0.03, freqmax=10, corners=8, zerophase=True)
ra_orig = ss.copy()
ra_orig.integrate() # original rotation angle recording (source)
ts = ss.copy()
ts.integrate() # source for correction (tilt angle recording)
# In this example, we are treating the North-axis of acceleration and the
# East-axis of rotation angle. Thus, for a positive rotation, the tilt induced
# accelertion shows into the same direction as the horizontal ground movement
# accelertion. We account for this in the subsequent analysis by setting
par = True
# -----------------------------------------------------------------------------
# now, lets do the tilt corrections
#
# frequency domain (coh)
# -----------------------------------------------------------------------------
fmin = None
fmax = None
acc_corr_freq1_data = remove_tilt(
rf1[0].data, ts[0].data, rf1[0].stats.delta, fmin, fmax,
parallel=par, smooth=100./164., method='coh')
acc_corr_freq1 = acc_orig.copy()
acc_corr_freq1[0].data = acc_corr_freq1_data
acc_corr_freq1.detrend('demean')
vel_corr_freq1 = acc_corr_freq1.copy()
vel_corr_freq1.integrate()
# -----------------------------------------------------------------------------
# frequency domain (plain)
# -----------------------------------------------------------------------------
fmin = None
fmax = None
acc_corr_freq2_data = remove_tilt(
rf2[0].data, ts[0].data, rf2[0].stats.delta, fmin, fmax,
parallel=par, smooth=100./164., method='freq')
acc_corr_freq2 = acc_orig.copy()
acc_corr_freq2[0].data = acc_corr_freq2_data
acc_corr_freq2.detrend('demean')
vel_corr_freq2 = acc_corr_freq2.copy()
vel_corr_freq2.integrate()
# -----------------------------------------------------------------------------
# time domain
# -----------------------------------------------------------------------------
acc_corr_time_data = remove_tilt(
rt[0].data, ts[0].data, rt[0].stats.delta, parallel=par)
acc_corr_time = acc_orig.copy()
acc_corr_time[0].data = acc_corr_time_data
acc_corr_time.detrend('demean')
vel_corr_time = acc_corr_time.copy()
vel_corr_time.integrate()
# Due to the very well known geometry in the tilt table experiment, we can play
# some games e.g. try to locate the proof mass of the seismometer and compare
# the output of our corrections with theortically expercted movements.
# get the time stamps of the beginning and end of the steps
on, off = trigger(
rr_orig[0], 10, 140, 6.0, 5.0, c_on, c_off, S, E,
plot_flagg=False)
# define a time axis
sec = np.arange(len(acc_orig[0].data))/(acc_orig[0].stats.sampling_rate)
print(len(on))
print(len(off))
# calculate residual displacement
alpha = get_angle(ts, on, off) # angle steps recorded by BS1
# in theory: according to Steffen position of the mass is approximately at the
# middle of the housing
h_m = 0.0575 # m
h = h_m # m
std_m = 0.01
r, centr = theo_resid_disp(ts[0].data, l, h, dh, rr_orig[0].data)
trr = Stream(traces=Trace(data=r, header=ts[0].stats))
trr.differentiate()
trr_a = trr.copy()
trr_a.differentiate()
time_ttheo, disp_ttheo, mean_disp_ttheo, sigma_ttheo = calc_residual_disp(
trr, on, off, np.zeros(len(r)), theo=True)
h_ttheo, std_ttheo = calc_height_of_mass(mean_disp_ttheo, l, dh, alpha)
tcentr = Stream(traces=Trace(data=centr, header=ts[0].stats))
tcentr.detrend('demean')
tcentr.detrend('linear')
tcentr.integrate()
tcentr.detrend('demean')
tcentr.detrend('linear')
tcentr.integrate()
# correct for residual displacement in time domain
acc_corr_time2 = acc_corr_time.copy()
acc_corr_time2[0].data = acc_corr_time2[0].data - trr_a[0].data
vel_corr_time2 = acc_corr_time2.copy()
vel_corr_time2.integrate()
tr1_vel = vel_corr_freq1.copy()
tr2_vel = vel_corr_freq2.copy()
tt_vel = vel_corr_time.copy()
tt2_vel = vel_corr_time2.copy()
tr1_new = vel_corr_freq1.copy()
tr2_new = vel_corr_freq2.copy()
tt_new = vel_corr_time.copy()
tt2_new = vel_corr_time2.copy()
time_tr1, disp_tr1, mean_disp_tr1, sigma_tr1 = calc_residual_disp(
tr1_new, on, off, r)
time_tr2, disp_tr2, mean_disp_tr2, sigma_tr2 = calc_residual_disp(
tr2_new, on, off, r)
time_tt, disp_tt, mean_disp_tt, sigma_tt = calc_residual_disp(
tt_new, on, off, r)
time_tt2, disp_tt2, mean_disp_tt2, sigma_tt2 = calc_residual_disp(
tt2_new, on, off, r)
# calculate the position of the seismometer mass #
##################################################
h_tr1, std_tr1 = calc_height_of_mass(mean_disp_tr1, l, dh, alpha)
h_tr2, std_tr2 = calc_height_of_mass(mean_disp_tr2, l, dh, alpha)
h_tt, std_tt = calc_height_of_mass(mean_disp_tt, l, dh, alpha)
disp_corr_freq1 = vel_corr_freq1.copy()
disp_corr_freq1.integrate()
disp_corr_freq2 = vel_corr_freq2.copy()
disp_corr_freq2.integrate()
disp_corr_time = vel_corr_time.copy()
disp_corr_time.integrate()
disp_corr_time2 = vel_corr_time2.copy()
disp_corr_time2.integrate()
# -----------------------------------------------------------------------------
# OUTPUT
# -----------------------------------------------------------------------------
scale = 1.e3
scaled = 1.e6
print('-----------------------------------------------')
print('mean residual displacement:')
print('frequency domain (coh): %.3f +/- %.3f mm' % (
mean_disp_tr1*scale, sigma_tr1*scale))
print('frequency domain (CaW): %.3f +/- %.3f mm' % (
mean_disp_tr2*scale, sigma_tr2*scale))
print('time domain : %.3f +/- %.3f mm' % (
mean_disp_tt*scale, sigma_tt*scale))
print('')
print('-----------------------------------------------')
print('height of seismometer mass:')
print('frequency domain (coh): %.3f +/- %.3f mm' % (
h_tr1*scale, std_tr1*scale))
print('frequency domain (CaW): %.3f +/- %.3f mm' % (
h_tr2*scale, std_tr2*scale))
print('time domain : %.3f +/- %.3f mm' % (
h_tt*scale, std_tt*scale))
print('theoretical : %.3f +/- %.3f mm' % (
h_ttheo*scale, std_ttheo*scale))
print('measured : %.3f +/- %.3f mm' % (
h_m*scale, std_m*scale))
print('-----------------------------------------------')
print('')
# -----------------------------------------------------------------------------
# PLOTS
# -----------------------------------------------------------------------------
# uncomment the following lines in case you want to use latex for type setting
# params = {
# 'text.usetex': True,
# 'text.latex.preamble': [
# r'\usepackage{cmbright}', r'\usepackage{amsmath}']}
# plt.rcParams.update(params)
# -----------------------------------------------------------------------------
plt.rcParams['figure.figsize'] = 7.1, 9.6
sizeOfFont = 12
fontProperties = {'weight': 'normal', 'size': sizeOfFont}
rc('font', **fontProperties)
# -----------------------------------------------------------------------------
# colors and linestyles
# define colors
al_trig = 0.1
c_trig_on = (0, 0, 0)
c_trig_off = (0, 0, 0)
c_angle = (1, 0, 0)
c_vel = (0, 0, 0)
c_time = (0, 0, 1)
c_time2 = (0, 0.8, 1)
c_coh = (1, 0.54, 0)
c_freq = (0, 0.8, 0)
c_tdisp = (0, 0, 0)
# define linestyles
ls_trig_on = '-'
ls_trig_off = '-'
ls_angle = '-'
ls_vel = '-'
ls_time = '-'
ls_time2 = '--'
ls_coh = '--'
ls_freq = ':'
ls_tdisp = ':'
# define linewidth
lw_trig_on = 2.0
lw_trig_off = 2.0
lw_angle = 2.0
lw_vel = 2.0
lw_time = 1.5
lw_time2 = 1.5
lw_coh = 2.5
lw_freq = 2.5
lw_tdisp = 2.0
# define labels
l_trig = 'step table movement'
l_angle = 'tilt angle'
l_vel = 'NOT corrected'
l_time = 'corr. time domain'
l_time2 = 'corr. time domain with disp'
l_coh = 'corr. frequency domain (adapted)'
l_freq = 'corr. frequency domain (CaW2000)'
l_tdisp = 'theo. displacement'
# END colors and linestyles
#############################################################################
gridspec = dict(hspace=0.0, height_ratios=[1, 1, 0.2, 1, 1])
fig, axs = plt.subplots(nrows=5, ncols=1, gridspec_kw=gridspec)
axs[2].set_visible(False)
ax0 = axs[0]
ax2 = axs[1]
ax3 = axs[3]
ax31 = ax3.twinx()
ax4 = axs[4]
line_angle, = ax0.plot(
sec, ts[0].data*scale,
color=c_angle,
linestyle=ls_angle,
linewidth=lw_angle,
label=l_angle)
for i in range(len(on)):
p_trig = ax0.axvspan(
on[i], off[i],
alpha=al_trig,
color=c_trig_on)
line_vel, = ax2.plot(
sec, vel_orig[0].data*scale,
color=c_vel,
linestyle=ls_vel,
linewidth=lw_vel,
label=l_vel)
line_time, = ax2.plot(
sec, tt_vel[0].data*scale,
color=c_time,
linestyle=ls_time,
linewidth=lw_time,
label=l_time)
for i in range(len(on)):
ax2.axvspan(
on[i], off[i],
alpha=al_trig,
color=c_trig_on)
line_angle, = ax31.plot(
sec,
ts[0].data*scale,
color=c_angle,
linestyle=ls_angle,
linewidth=lw_angle,
label=l_angle)
for i in range(len(on)):
p_trig = ax31.axvspan(
on[i], off[i],
alpha=al_trig,
color=c_trig_on)
line_time, = ax3.plot(
sec, tt_vel[0].data*scale,
color=c_time,
linestyle=ls_time,
linewidth=lw_time, label=l_time)
line_coh, = ax3.plot(
sec, tr1_vel[0].data*scale,
color=c_coh,
linestyle=ls_coh,
linewidth=lw_coh,
label=l_coh)
line_freq, = ax3.plot(
sec, tr2_vel[0].data*scale,
color=c_freq,
linestyle=ls_freq,
linewidth=lw_freq,
label=l_freq)
line_time2, = ax3.plot(
sec, vel_corr_time2[0].data*scale,
color=c_time2,
linestyle=ls_time2,
linewidth=lw_time2,
label=l_time2)
for i in range(len(on)):
ax4.axvspan(
on[i], off[i],
alpha=al_trig,
color=c_trig_on)
line_time_d, = ax4.plot(
time_tt[i],
disp_tt[i]*scaled,
color=c_time,
linestyle=ls_time,
linewidth=lw_time,
label=l_time)
line_coh_d, = ax4.plot(
time_tr1[i],
disp_tr1[i]*scaled,
color=c_coh,
linestyle=ls_coh,
linewidth=lw_coh,
label=l_coh)
line_freq_d, = ax4.plot(
time_tr2[i],
disp_tr2[i]*scaled,
color=c_freq,
linestyle=ls_freq,
linewidth=lw_freq,
label=l_freq)
line_time_d2, = ax4.plot(
time_tt2[i],
disp_tt2[i]*scaled,
color=c_time2,
linestyle=ls_time2,
linewidth=lw_time2,
label=l_time2)
line_theo_d, = ax4.plot(
sec,
r*scaled,
color=c_tdisp,
linestyle=ls_tdisp,
label=l_tdisp)
ax0.set_ylabel('rotation angle [mrad]', color=c_angle)
ax2.set_ylabel('velocity [mm/s]')
ax3.set_ylabel('velocity [mm/s]')
ax31.set_ylabel('rotation angle [mrad]', color=c_angle)
ax4.set_ylabel('displacement [mum]')
ax4.set_xlabel('time [s]')
ax0.tick_params('y', colors=c_angle)
ax31.tick_params('y', colors=c_angle)
ax0.tick_params(direction='in')
ax2.tick_params(direction='in')
ax3.tick_params(direction='in')
ax31.tick_params(direction='in')
ax4.tick_params(direction='in')
ax0.set_xticklabels([])
ax31.set_xticklabels([])
ax3.set_xticklabels([])
ax0.text(-16, 0.26, '(a)')
ax3.text(53.32, 0.13, '(b)')
# legend
ba = (-0.098, 3.2)
lines = (
p_trig, line_angle, line_vel, line_theo_d, line_coh, line_freq, line_time,
line_time2)
labels = (l_trig, l_angle, l_vel, l_tdisp, l_coh, l_freq, l_time, l_time2)
plt.legend(
lines, labels,
loc=ba,
bbox_transform=None,
borderaxespad=0.,
frameon=False,
ncol=2)
ax0.set_xlim(zoom00, zoom01)
ax2.set_xlim(zoom00, zoom01)
ax3.set_xlim(zoom0, zoom1)
ax31.set_xlim(zoom0, zoom1)
ax4.set_xlim(zoom0, zoom1)
plt.subplots_adjust(
top=0.868,
bottom=0.053,
left=0.118,
right=0.88)
zoom_effect01(ax2, ax3, 54.16, 55.00)
plt.gcf().savefig('tilt_correction_step_table.png')
plt.show()